Mundo Matemático: ¿Cuánta es la gravedad de la Luna?

Es posible que al hablar de la Luna también se hable de la gravedad. Pero… ¿qué es eso? Para responder a esa pregunta y la relación de la gravedad con nuestro planeta y nosotros está Mundo Matemático. Agarra tu cuaderno y toma nota de todo lo que te explicaremos a continuación.

¿Qué es la gravedad?

La gravedad es la fuerza que un cuerpo de mayor masa ejerce sobre otro. Este concepto también implica otros que no podemos dejar de aprender, uno de ellos es el peso. Esto es equivalente a la magnitud de la fuerza con la que nos atrae la Tierra o la Luna, en el caso de que nos encontremos en ella. 

 Peso = masa x gravedad

*Valor de gravedad en la Tierra: 9,8 m/s2 

Ley de Gravitación Universal

Isaac Newton postuló que todas las masas se atraen entre sí. Claro que esto aplica para masas de gran fuerza y no masas de fuerza muy débil como las que surgen entre las personas. Una de las masas de gran fuerza es la Tierra, cuya fuerza logra mantenernos unidos al suelo y no flotar. Aunque… sería divertido, ¿no creen?

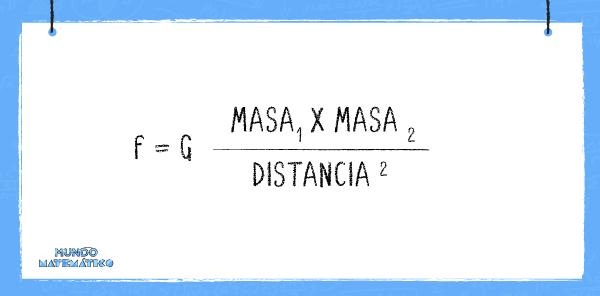
De acuerdo con esta fórmula, la fuerza de atracción aumenta en proporción directa a las masas. Así cuando hay mayor masa, hay mayor atracción. Sin embargo, cuando la proporción se da de manera inversa, la fórmula anterior se puede reducir a:

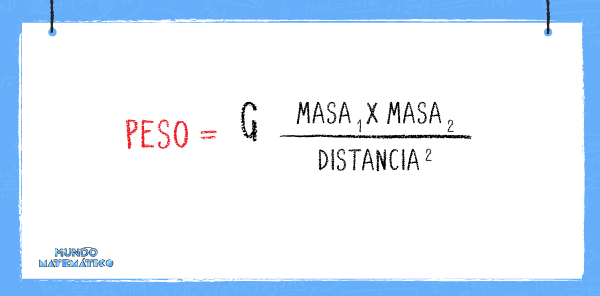
La “G”, que es la constante de gravitación que equivale a la fuerza entre dos masas de un 1 kilogramo a 1 metro de distancia tiene el siguiente valor:

 6,7 x 10-11

En el caso de la Luna, su masa equivale a:

7,349 x 1022

En los valores anteriores podemos encontrar números pequeños en color rojo. Estos son exponentes, los cuales nos indicarán cuántas veces se repetirá el valor en la operación. En efecto, antes de poder calcular la gravedad, es necesario que aprendas la teoría de exponentes. De esta manera el ejercicio que te mostraremos será muy fácil.

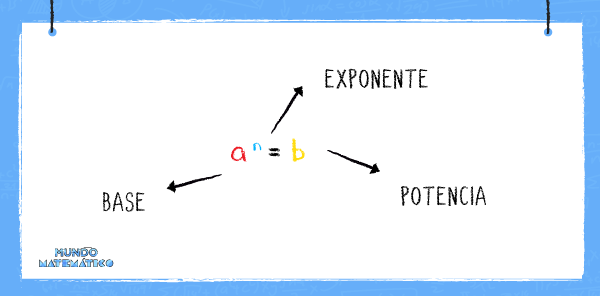
Teoría de exponentes

En la teoría de exponentes encontramos 3 propiedades. La primera dice que cuando las bases son iguales, los exponentes se suman. La segunda propiedad menciona que en una fracción de bases iguales, los exponentes se restan. Finalmente, la tercera nos dice que cuando una potencia se eleva a la potencia, sus exponentes se multiplican.

¡Calculemos la gravedad!

Ahora sí es momento de calcular la gravedad con un ejemplo que seguro te interesa saber. ¿En cuánto se reduce el peso de un astronauta en la Luna en relación al peso que tienen en la Tierra?

Para hallar el peso necesitamos conocer la masa y la gravedad. Aunque el astronauta esté en la Luna su masa no cambia. Si prestaste atención recordarás que la gravedad de la Tierra es 9,8 m/s2. Ahora solo necesitamos encontrar la gravedad de la Luna.

Para encontrarla aplicamos la fórmula de Newton que vimos previamente: 

Debemos reemplazar los valores de las masas:

masa1= masa del astronauta

masa2 = masa de la Luna

distancia = radio de la Luna

El peso sería la masa del astronauta (masa1) multiplicada por la gravedad de la luna:

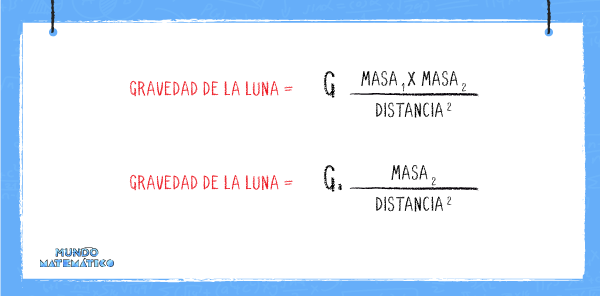
Reemplazamos la constante de gravitación y la masa de la Luna:

G =6,7 x 10-11

Masa2 = masa de la Luna = 7,349 x 1022

Distancia = 1 737 km = 1 737 000 m = 1,737 x 106

Ahora, reemplazamos estos valores en la fórmula que nos permitirá hallar la gravedad de la luna.

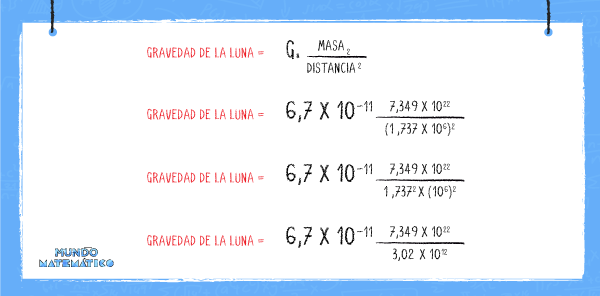
Recordando las propiedades de los exponentes que vimos anteriormente resolvemos la ecuación:

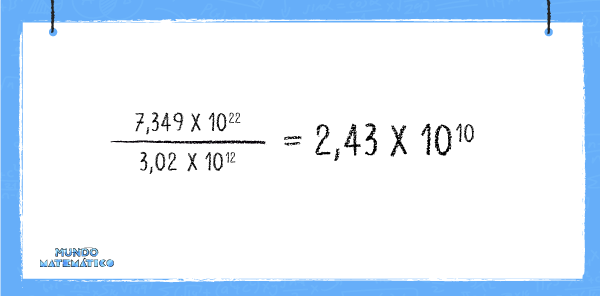
Multiplicamos el resultado obtenido por la constante de gravitación:

gravedad de la Luna = 6,7 x 10-11x 2,43 x 1010

gravedad de la Luna = 16,28 x 10-1

gravedad de la Luna = 16,28 x 1/10

gravedad de la Luna = 1,628 ≈ 1,62

Este resultado nos indica que la gravedad de la Tierra es 9,8 y la gravedad de la Luna es 1,62. Al dividir ambas gravedades obtenemos 6,04, lo que significa que la gravedad de la Tierra es 6 veces mayor a la de la Luna. De esto se desprende que el peso del astronauta en la Tierra será seis veces más que en la Luna. ¡Vayamos a la Luna!

¡Qué interesante episodio! No te pierdas todo lo que Mundo Matemático tiene preparado para ti de lunes a viernes a las 8:00 p. m. y los sábados y domingos a las 6:30 p. m. por la señal de Canal IPe.