Televisión · 15 de Dic 2020
Mundo Matemático: El sonido y las matemáticas
Mundo Matemático nos enseña a medir las ondas a través de la función trigonométrica “seno”.

Pexels/Canal IPe
Si tocas la guitarra, o has visto a alguien tocarla, seguro notaste cómo vibran las cuerdas al rasguear. Esta vibración hace posible el sonido que necesita de una fuente como también pueden ser las cuerdas vocales, las cuerdas del violín o las patas de los grillos.
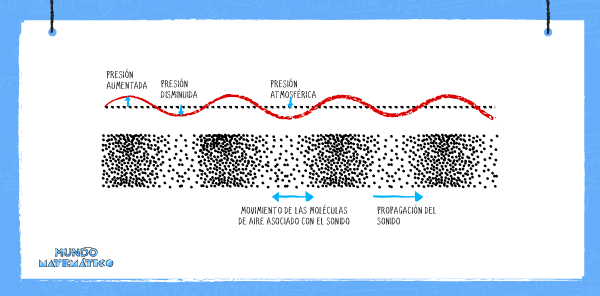
La vibración genera el movimiento (ondulatorio) de partículas, las cuales van de ida y de vuelta, pero en el trayecto chocan entre sí y transmiten energía. Las ondas que se generan pueden tener picos altos (mayor valor) y picos bajos (menor valor). Esto sucede por la presión que surge cuando las partículas se juntan. Para describir esta característica de la onda utilizaremos la función trigonométrica seno, la cual Mundo Matemático te explicará a continuación.
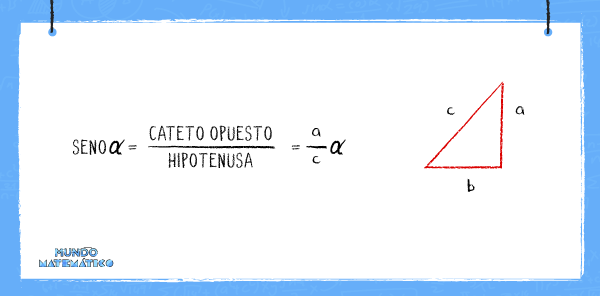
Calculemos la función Seno α
En el triángulo rectángulo el seno de un ángulo equivale a la relación entre la hipotenusa y el cateto opuesto al ángulo.
Si colocamos el triángulo rectángulo en una circunferencia de radio 1, la hipotenusa sería el radio y el seno sería el siguiente segmento vertical:
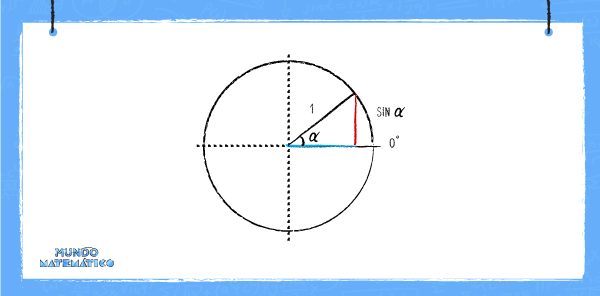
Si el valor del ángulo seno tiene una variación, el segmento vertical (cateto opuesto) también sufrirá una variación. Si el ángulo disminuye, el valor del segmento vertical va a disminuir. Si el ángulo aumenta y nuestra hipotenusa llega hasta los 90°, este será equivalente a 1, de acuerdo con la información anterior.
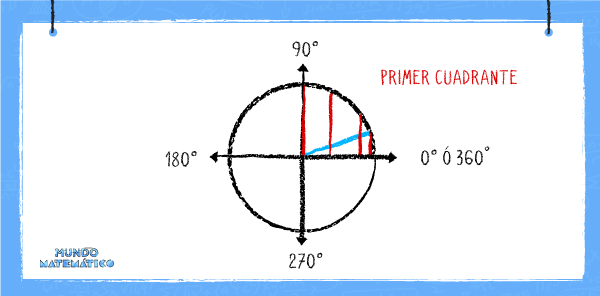
Si la hipotenusa gira hacia la izquierda, es decir, si pasa al segundo cuadrante, el valor de ángulo seno disminuirá. En este ejemplo lo hará de manera simétrica como el ejemplo anterior.
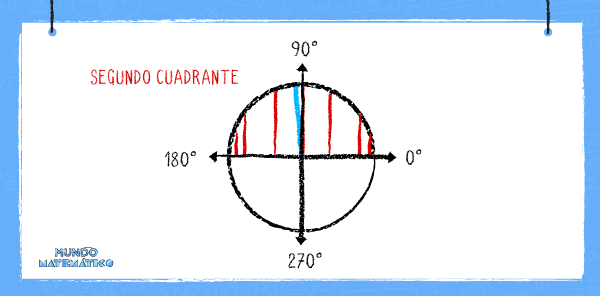
Ahora vamos a representar los valores de la función seno en una gráfica de coordenadas. En el eje horizontal (x) colocaremos la medida de los ángulos y en el eje vertical (y) colocaremos la medida del segmento vertical que obtuvimos al ir cambiando de ángulo en el primer cuadrante.
Ahora, hacemos lo mismo de acuerdo a los valores obtenidos en el segundo cuadrante.
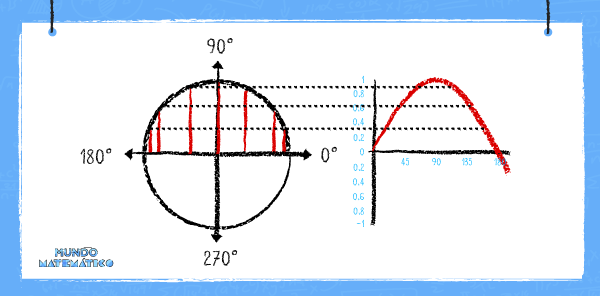
La función seno, representa la onda longitudinal que recorre el sonido. Cuando se acerca a 90° aumenta la presión de las partículas. Cuando se acerca a 0° no surge ni mucha presión, ni poca presión, hay un estado de equilibrio.
Ya representamos los valores de los cuadrantes superiores. Ahoram, lo haremos con el tercer y cuarto cuadrante.
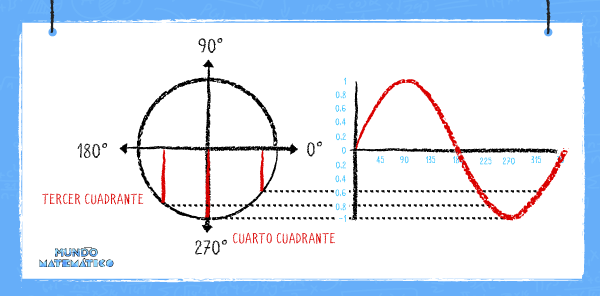
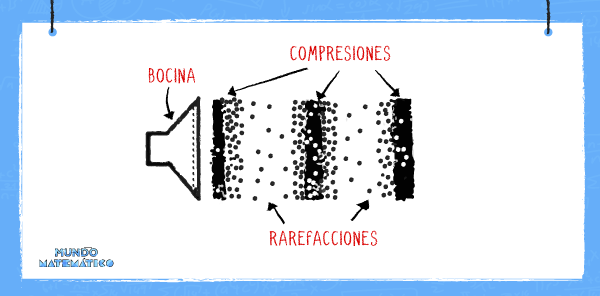
Todas las gráficas anteriores muestran que la función seno es periódica. Su máximo valor es 1 y su valor mínimo es -1. El periodo se cumple al terminar la vuelta, es decir cuando se cumple 360°. Así, la función seno representa el movimiento ondulatorio del sonido a mayor valor (compresión) y menor valor rarefacción y el periodo de tiempo que dura.
Las ondas que vemos al hacer grabaciones representan todo el proceso anterior.
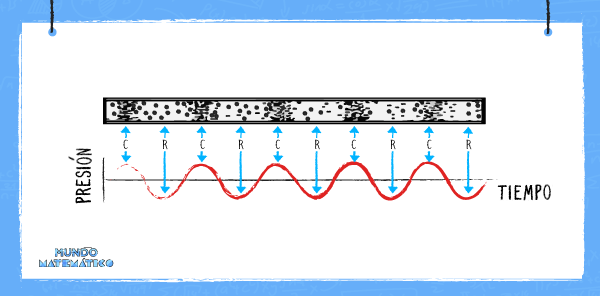
La oscilación periódica de las partículas del mayor valor al menor es el ciclo. El tiempo de cada una es el periodo (T), el cual se mide en segundos y el número de ciclos que se dan por segundo representan la frecuencia (f), la cual se mide en Hertz (Hz).
En la siguiente gráfica cada periodo mide ⅓ de segundo y se dan 3 ciclos por segundo lo que significa que la frecuencia será igual a 3 Hertz.
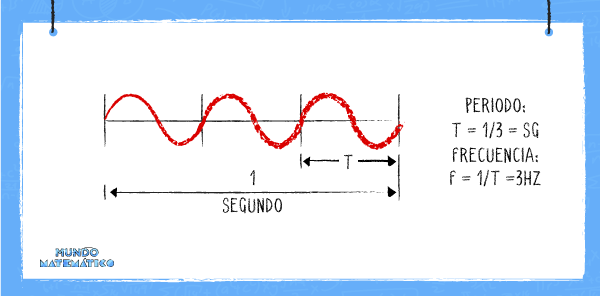
De eso se deduce que a menos periodo de oscilación, mayor será la frecuencia. Si las curvas están más juntas la frecuencia será mayor, como se representan las notas agudas. Por el contrario, cuando las curvas están más separadas, la frecuencia será menor, como lo representa la gráfica de las notas graves.
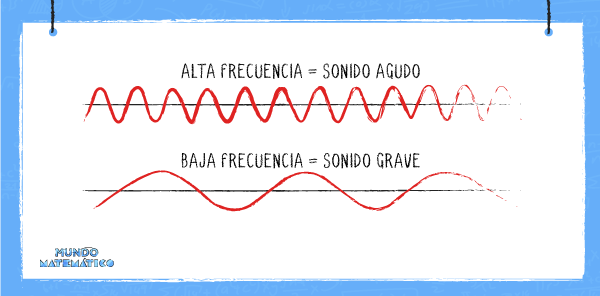
Ahora que sabes cómo utilizar la función trigonométrica seno y representar el sonido podrás resolver todos los problemas que te manden de tarea.
Para seguir practicando no te pierdas este y todos los episodios de Mundo Matemático los lunes, martes y miércoles a las 8:00 p. m. y los sábados y domingos a las 6:30 p. m. por la señal de Canal IPe. Si se perdieron este episodio también pueden verlo en nuestro canal de YouTube de Canal IPe.









