Televisión · 22 de Dic 2020
Mundo Matemático: ¿Cómo se mide la capacidad de los pozos?
Aprende a calcular la medida de un pozo con ayuda de Mundo Matemático.

Pixabay/Canal IPe
La Tierra está compuesta por agua… ¡mucha agua! El 97% del agua que tiene el planeta es salada y solo el 3% es dulce. El agua de los ríos, lagunas y lagos representan el 0,03% de ese 3% de agua dulce y el 0,6% es agua subterránea.
Sí, hay agua que viene del subsuelo y puede ser de mucha utilidad. Los Nazca aprovechaban esa agua a través de un sistema hidráulico de puquios, pozos y acueductos. ¿Quieres saber cómo se mide la capacidad de un pozo? Agarra tu cuaderno y toma nota, que Mundo Matemático te enseñará a continuación:
Así se miden los pozos
Para determinar la capacidad de un pozo vamos a calcular primero su volumen. Este volumen debe ser convertido en litros.
1m3 = 1000 litros

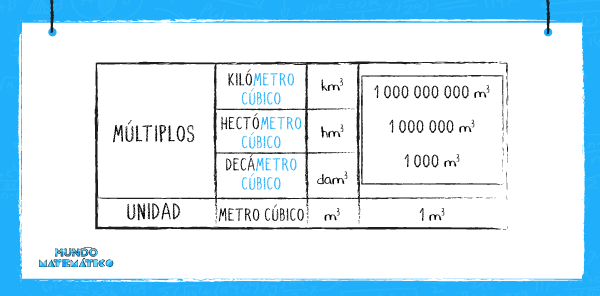
Las reservas explotables de agua subterránea de un valle o zona puede llegar hasta los hectómetros cúbicos.
El agua subterránea de un valle y otras zonas pueden tener medidas altas, hasta hectómetros cúbicos, es decir, millones de metros cúbicos, que equivalen a miles de millones de litros.
El volumen del pozo se calcula con la siguiente fórmula:
V = área de la base x altura
El área de la base equivale al área del círculo:
V = πrr2 ∙ h
La altura (h) sería la profundidad, la cual mediremos con ayuda de las ecuaciones de segundo grado y dos principios físicos. También nos ayudará una piedra… Sí, lanzaremos una piedra dentro del pozo para que, a través de las vibraciones de aire (onda sonora), que surgen en el choque de la piedra con el suelo, podamos calcular la profundidad. De este hecho se desprende la gravedad (g) con la que cae la piedra, que para este caso será 9,8 m/s2 y la fórmula de caída libre con velocidad inicial igual a cero (Vo). En este caso la aceleración es igual a la gravedad.

En la ecuación anterior obtenemos una ecuación cuadrática, por lo que debemos recordar su fórmula:
ax2 + bx + c = 0
Asimismo debemos tomar en cuenta su fórmula:
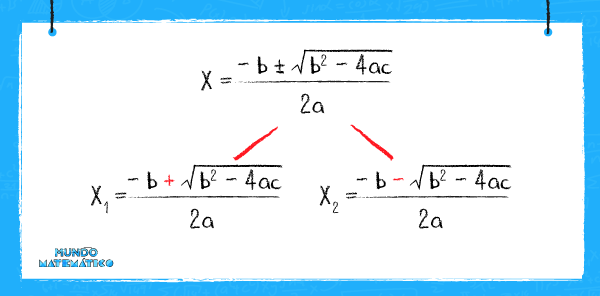
Si todavía no queda claro, no te preocupes. Vamos a resolver un ejercicio para que no quede ninguna duda.
Si dejamos caer una piedra en un pozo vacío, su impacto con el suelo sonará luego de 1,6 segundos. Si el diámetro del pozo es 4 metros. ¿Cuántas familias tendrán agua si esta se encuentra al tope máximo del pozo? Se nos indica que cada familia consume un aproximado de 150 litros diarios y que la medida de la velocidad del sonido es de 340 m/s.
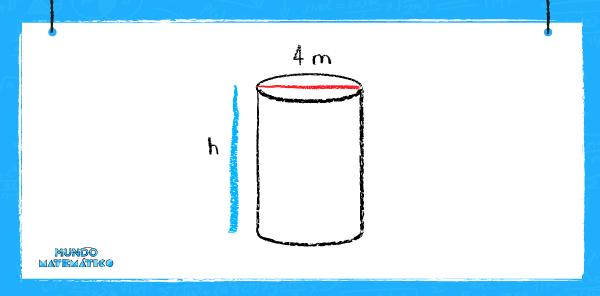
Calcularemos el volumen y la capacidad del pozo. Se nos ha dado el valor del radio, pero también necesitamos la altura.
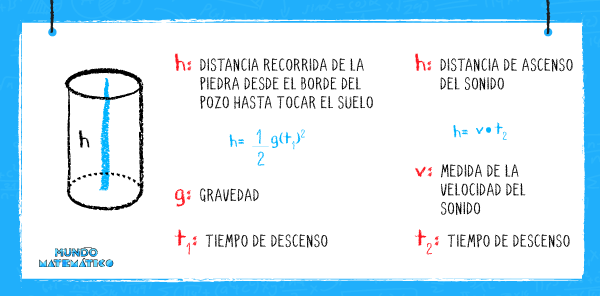
Entonces obtenemos la siguiente ecuación (ecuación 1):
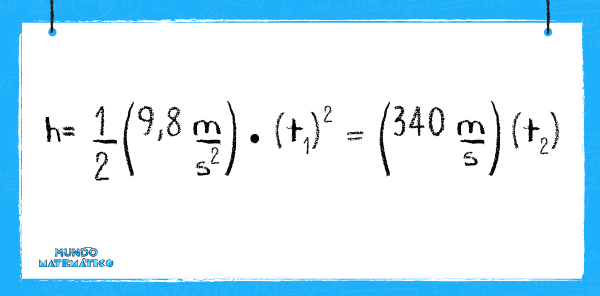
Observamos dos valores de tiempo, los cuales equivalen al tiempo total. Este es igual al tiempo de descenso (t1) sumado al tiempo de ascenso (t2). Vamos a obtener una ecuación a la que denominaremos “ecuación 2”:
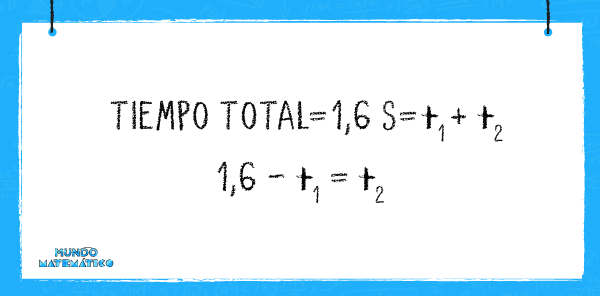
Ahora vamos a desarrollar la primera ecuación. reemplazamos “t2” e igualamos la ecuación a “0”. Con el resultado formamos una ecuación cuadrática.

Ahora aplicamos la última fórmula que vimos antes de comenzar el ejercicio:

De acuerdo al resultado anterior, podemos obtener 2 posibles respuestas:
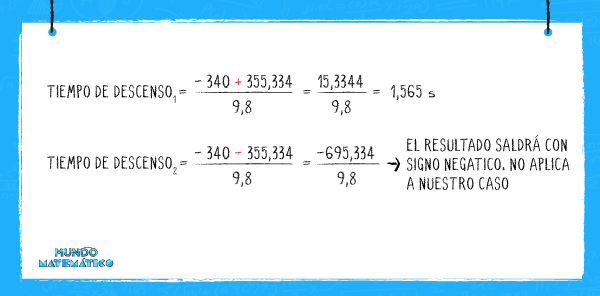
Si el tiempo de descenso es igual a 1565, el ascenso del sonido será 0,053 s. Entonces aplicamos la siguiente fórmula:

Con este resultado obtenemos que el volumen del pozo es:
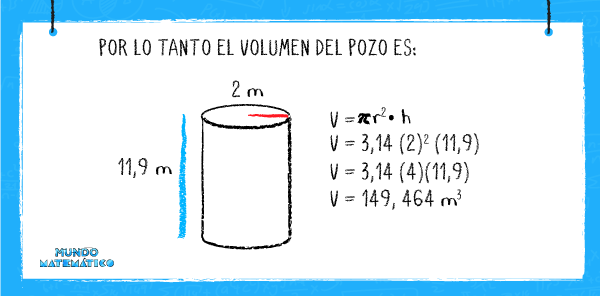
Transformamos los metros cúbicos a litros:
1 m3 = 1 000 litros
149,464 m3 x 1 000= 149 464 litros
Se nos dijo al inicio del ejercicio que cada familia consume 150 litros diarios, entonces, de acuerdo a esta condición el pozo completo alcanzaría aproximadamente para 996 familias por día:
149 464 : 150 = 996, 4 familias ≈ 996 familias por día
Resolviendo ejemplos aprenderemos las fórmulas de manera más fácil. Si quieren seguir aprendiendo más conceptos y fórmulas no dejen de ver Mundo Matemático de lunes a viernes a las 8:00 p. m. y los sábados y domingos a las 6:30 p. m. por la señal de Canal IPe.









