Mundo Matemático: ¿Cuál es la proporcionalidad compuesta?

Como consecuencia de la pandemia la fabricación de implementos de protección aumentó considerablemente. Debido a que su demanda es grande, la producción debe serlo también. Esto se puede medir gracias a que son magnitudes.

¿En qué consisten las magnitudes?

Las magnitudes son características medibles. Por ejemplo, pueden ser un determinado número de personas, la estatura de alguien, el número de horas que nos demoramos en comer y más. 

Magnitudes directamente proporcionales

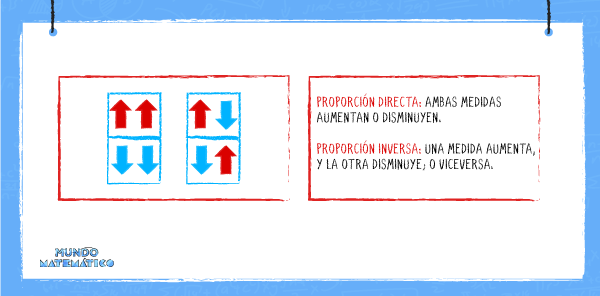
Las magnitudes pueden ser directamente proporcionales (D.P.). Esto sucede cuando la medida de una aumenta y por ende la medida de la otra magnitud también, en la misma proporción que la primera. Es decir que, si la primera medida se triplica, la segunda también se triplicará. Lo mismo ocurre si en lugar de aumentar, disminuye. Siempre con la misma proporción.

Te mostramos un ejemplo para que quede más claro que el agua mineral. 

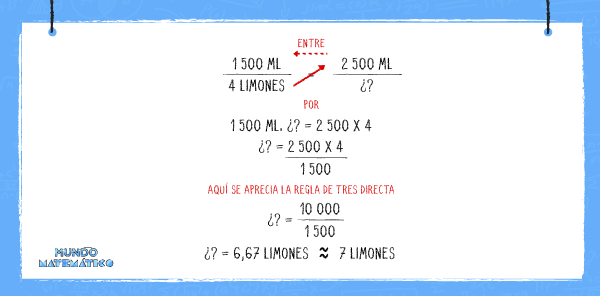
Para preparar un litro y medio de limonada (1500 ml) se requieren 4 limones. Así tenemos:

En este tipo de proporcionalidad el cociente de las medidas es el mismo. En el siguiente ejemplo el valor 375 es la constante de proporcionalidad directa.

Con la información que plantea el problema hallaremos el número de limones que se requieren para 2,5 litros de agua. También transformaremos este valor de litros a mililitros. 

Magnitudes inversamente proporcionales

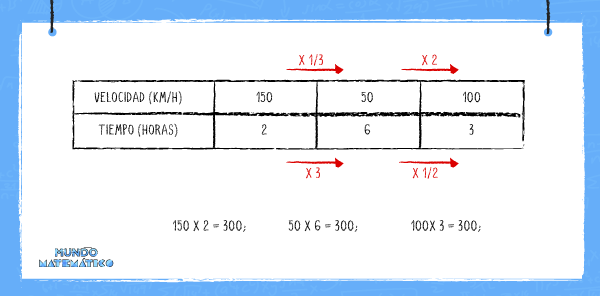
A diferencia de las magnitudes directamente proporcionales, las magnitudes inversamente proporcionales (I.P.) plantean que cuando aumenta la medida de una magnitud, la medida de la otra disminuye. A pesar de que se aplicarán operaciones distintas, la proporción en la que se aplicará será la misma. Es decir, si una medida se multiplica por 3, la otra medida se dividirá por 3.

¿No quedó muy claro? Acá te lo explicamos con un ejemplo. Digamos que para llegar de un punto A a un punto B en 2 horas, debemos desplazarnos a 150 Km/h. Si solo podemos hacerlo a 100 Km/ lo haremos en 3 horas. Y si nos desplazamos más despacio, a 50 Km/h tardaremos en llegar 6 horas.

De la igualdad anterior aplicamos la regla de 3 simple inversa para hallar las horas que se requiere viajar a 90 kh/h.

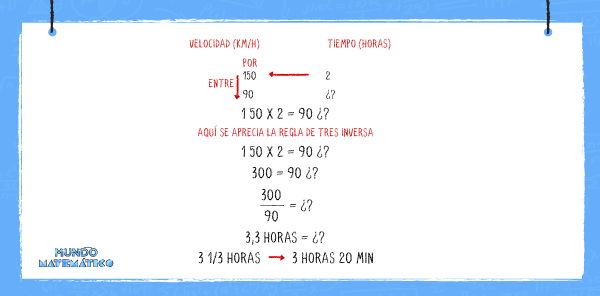
Aplicando la regla de tres inversa encontramos que el tiempo que se requiere para viajar es de 3 horas con 20 minutos.

Proporcionalidad compuesta

Para los ejemplos que hemos resuelto en los casos anteriores se consideraron dos magnitudes: proporcionalmente directa y proporcionalmente indirecta. Para hallar la medida de 3 o más magnitudes necesitaremos la proporcionalidad compuesta.

Para poder entender en qué consiste vamos a proponer el siguiente ejemplo.

En una sanguchería, que atiende a 100 comensales diarios en 6 horas, hay 2 personas cocinando. De acuerdo a esta información identificamos 3 magnitudes:

- El número de cocineros

- El número de comensales

- La cantidad de horas

La relación que hay entre el número de cocineros y el número de comensales es

directamente proporcional (D.P) . Si se triplica el número de personas que cocinan, también se triplicará el número de comensales.

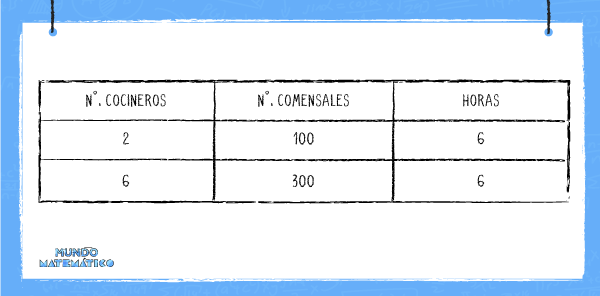
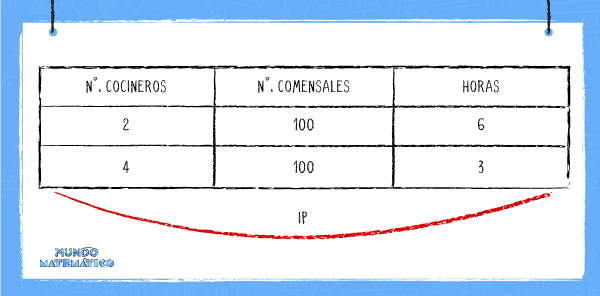
Por el contrario, la relación entre el número de cocineros y la cantidad de horas es inversamente proporcional (I.P.). Si duplico el número de cocineros, el tiempo de atención será la mitad.

Es momento de poner en práctica lo aprendido. Por eso no te pierdas este episodio de Mundo Matemático así como todos los demás de lunes a viernes a las 8:00 p. m. y los sábados y domingos a las 6:30 p. m. por la señal de Canal IPe.