Televisión · 09 de Dic 2020
Mundo Matemático: ¿Qué es la correlación lineal?
Mundo matemático te ayudará a calcular la relación de tus notas con el tiempo que le dedicas a estudiar.

Pixabay/Canal IPe
Los exámenes pueden ser complicados y es posible que otros factores afecten nuestro desempeño. Esto puede influir en nuestras notas, porque hay una relación entre ellas que podemos calcular matemáticamente a través de la correlación lineal. Agarra tu cuaderno, que Mundo matemático te enseñará en qué consiste.
La variable estadística cuantitativa
Para aprender sobre la correlación lineal es necesario conocer la variable estadística cuantitativa. Esta característica indica que algo se puede pedir, como una población de personas u objetos.
Cuando se analizan dos variables de la muestra, como la edad y estatura, esta se convierte en una variable estadística bidimensional.
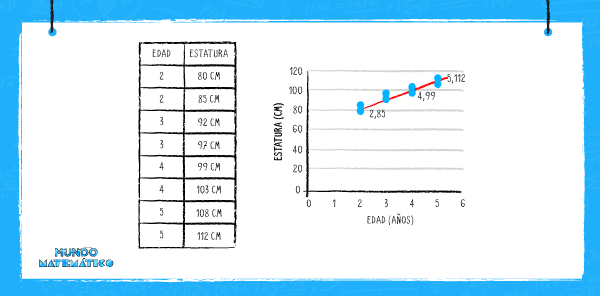
Los puntos que vemos en la gráfica anterior representan los dos valores de las variables. Si trazamos una línea que siga todos los puntos notaremos que aparece una recta, esta indica la relación lineal.
Sin embargo, la relación también puede ser no lineal, como la altura de los lápices y el puntaje de las notas de práctica de seis estudiantes. Esto se puede ver en el siguiente gráfico.
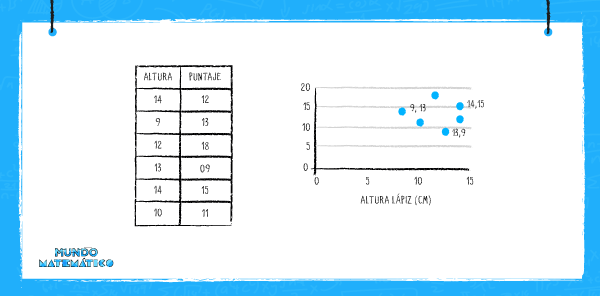
El gráfico anterior nos muestra una relación débil o nula de acuerdo a la posición de los puntos.
Covarianza
Así como necesitamos aprender sobre la variable estadística cuantitativa, también necesitamos aprender el concepto de covarianza. Este se encarga de medir el grado de dispersión conjunta de dos variables “X” e “Y”:
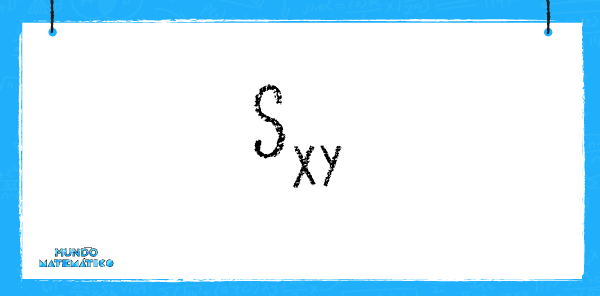
Para que quede claro vamos a calcularla, midiendo la altura y edad de 8 niños. Es necesario tomar en cuenta que para hallar la dispersión se necesita calcular la distancia a la media de cada variable.

Ahora tenemos que calcular la distancia de cada dato con respecto a su media y al obtenerla multiplicaremos esa diferencia.
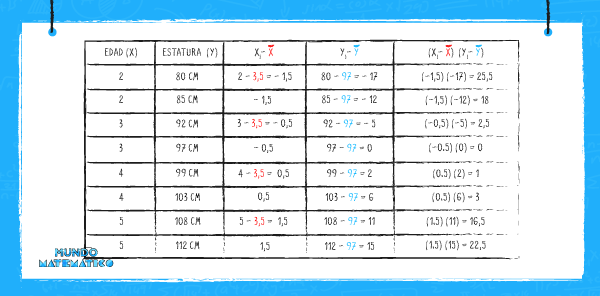
La media aritmética
Con el resultado anterior calcularemos la media aritmética o el promedio de los productos. Sumaremos dos datos de la última columna y lo dividiremos por el total.

¡Calculemos el coeficiente de correlación!
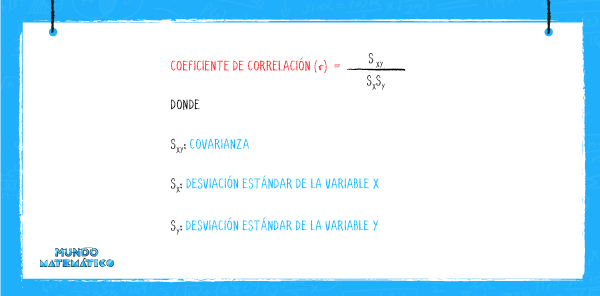
Es necesario tomar en cuenta que el coeficiente de correlación varía entre -1 y +1 ( -1< r < + 1). Si r = 1, la correlación es perfecta positiva, lo que quiere decir que la recta asciende. Por el contrario, si r = -1, la correlación es perfecta negativa y la recta desciende. Y, finalmente si r = 0, la correlación es nula.
Ahora calculemos la desviación estándar de “X”:
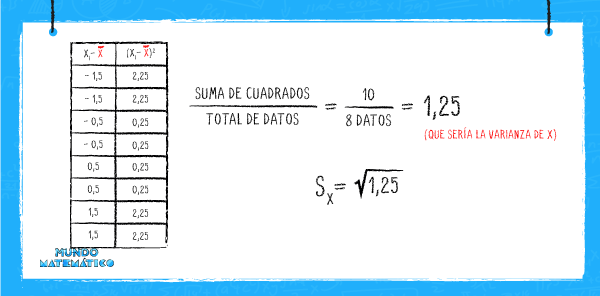
Seguido calculamos la desviación estándar de “Y”:
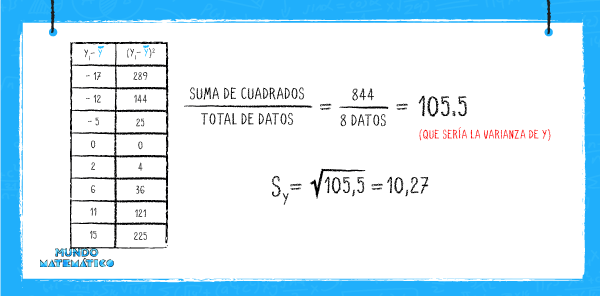
Con estos datos hallaremos el coeficiente de relación de las variables de niños de 2 a 5 años en cuanto a edad (X) y estatura (Y):
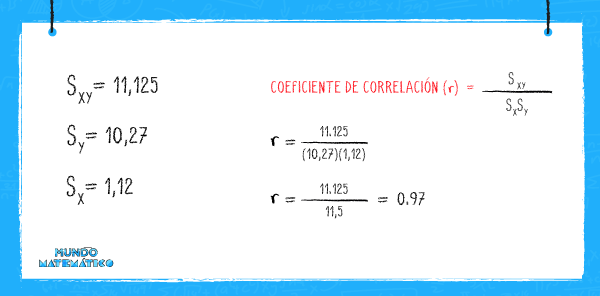
El valor que hemos obtenido es un valor de correlación cercano a “+1”. Esto quiere decir que las variables de los niños en tanto a edad y estatura tienen una dependencia lineal positiva marcada.
Es momento de aplicar estos conceptos, así que no te pierdas los ejercicios que Mundo Matemático tiene preparado en este episodio. No te pierdas todos los episodios de lunes a viernes a las 8:00 p. m. y los sábados y domingos a las 6:30 p. m.









