Televisión · 05 de Oct 2020
Mundo Matemático: ¿Qué es la desviación estándar y cómo calcularla?
Mundo Matemático nos enseña a calcular la desviación estándar. Si aún no te han enseñado, apunta lo que te enseñaremos en esta nota.
Canal IPe
Si ya estás a mitad de la secundaria es probable que te enseñen el concepto matemático de desviación estándar. Si aún no te enseñan en qué consiste o no lograste entender cómo calcularlo, Mundo Matemático podrá ayudarte. Así que abre tu cuaderno y presta atención a lo que te explicaremos a continuación.
Conceptos básicos para calcular la desviación estándar
La desviación estándar nos indica la medida de dispersión de los datos con respecto a la media. Es decir, qué tan dispersos están los datos de la media de los mismos.
¿Aún no queda claro? … Tranquilo, los ejemplos que te mostraremos te ayudarán a resolver cualquier duda. Pero antes de pasar a los ejemplos es necesario que sepas los conceptos matemáticos que nos ayudarán a calcular la desviación estándar. Estos son la media aritmética y la varianza.
Media aritmética
Es el promedio aritmético de los datos de una variable cualitativa. El concepto asusta, pero si lo ponemos en práctica es el resultado de la suma de datos entre el total de esos datos. Por ejemplo, si se suma la altura de 6 jugadores de vóley y se divide entre 6, el resultado sería la desviación estándar.
Tomando en cuenta que la altura de los jugadores son:
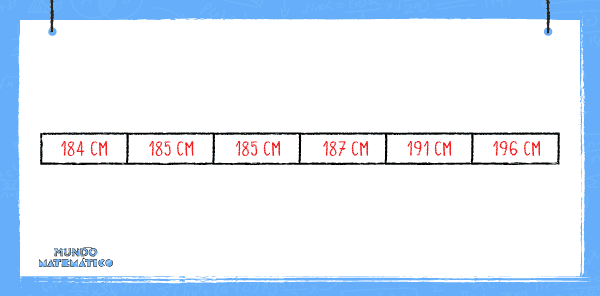
La desviación estándar se calculará de la siguiente manera:
X = (184 + 185 + 185 + 187 + 191 + 196) /6 = 188
La desviación estándar nos dice aquí que todos los jugadores miden 188 cm. Sin embargo, no todos los jugadores tienen esta estatura, sino que las medidas más extremas, como los jugadores de mayor altura, influyen en el cálculo de la media aritmética, la que en este caso aumenta. Para medir matemáticamente este hecho se utiliza la varianza.
Varianza
La varianza medirá el grado de dispersión de los datos, es decir, qué tanto varían los valores de los datos con respecto a su media aritmética.
Se calcula sumando las diferencias de cada dato con su media aritmética, las cuales son elevadas al cuadrado. Esta suma se divide entre el número de datos.
Siguiendo con el ejemplo anterior la varianza se calcula de la siguiente manera:
x = [(184 -188)2 + (185 - 188)2 + (185 - 188)2 + (187 - 188)2 + (191 -188)2 + (196 - 188)2]/6
x = 18
¡Calculemos la desviación estándar!
La desviación estándar es muy sencilla de calcular ya que es la raíz cuadrada de la varianza. Entonces, siguiendo con el ejemplo anterior la media aritmética será la raíz cuadrada de 18, es decir 4,24.
σ= √18= 4,24
La desviación estándar nos señala que la media se desvía en 4,24, así que la media aritmética que obtuvimos anteriormente se desvía entre 183,76 y 192,24, de acuerdo a las siguientes operaciones.
188 - 4,24 = 183,76 cm y 188 + 4,24 = 192,24
Esta medida se expresa de acuerdo al siguiente intervalo:
x = [183, 76; 192,24]
Para que sigas practicando y saques más veintes, te dejamos un problema sencillo para resolver.
Ejercicio: Calcula la varianza y desviación estándar de las estaturas de otro equipo de voley y determina el intervalo de variación de la media aritmética.
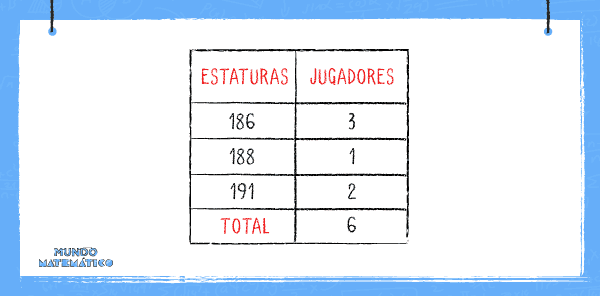
Cuéntanos si pudiste calcular todo lo que el ejercicio pide. Y no te pierdas todos los episodios de Munto Matemático de lunes a viernes a las 8:00 p. m. y los sábados y domingos a las 6:30 p. m. por la señal de Canal Ipe.
“ Aprender algo nuevo cada día es hermoso y más cuando es divertido”
No se pierda ningún artículo de
No te pierdas ningún artículo
