Televisión · 14 de Dic 2020
Mundo Matemático: ¿Qué son los fractales y la potencia de fracción?
Mundo Matemático nos enseña el misterio de las fractales. Descubre de qué trata en la siguiente nota.
Pexels/Canal IPe
¿Amas los videojuegos? Si tu respuesta es sí, es probable que no solo te guste jugarlos, sino que en algún momento también te ha interesado cómo se hacen. En el proceso de su creación hay muchas disciplinas, una de ellas es son las matemáticas. ¿Cómo las matemáticas pueden crear un videojuego? No te preocupes, que Mundo Matemático te explicará con detalle a través de las fractales.
Autosimilaridad
En la naturaleza ocurre algo llamado autosimilaridad. Ella explica que el pedazo de algo tendrá la misma forma y estructura que eso. Un ejemplo son las ramas de un árbol, cuando este se forma, sus ramificaciones se parece a las que brotaron antes:

Esta característica no solo nos la da la naturaleza, también lo hace la geometría fractal. Esta se aplica gracias a los ordenadores que crean diseños de muchas películas y videojuegos que conocemos hoy.
Fractales
Ahora que conocemos un poco de teoría vamos a enseñarte las fractales a través de un ejercicio. Pero antes de desarrollarlo, es necesario que sepas la siguiente fórmula:
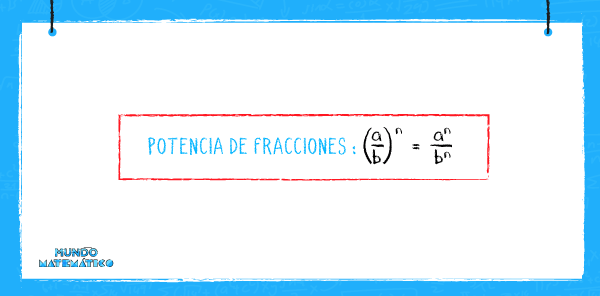
Tomemos en cuenta la siguiente imagen para explicar el patrón gráfico y hallar su área luego de la segunda fragmentación:
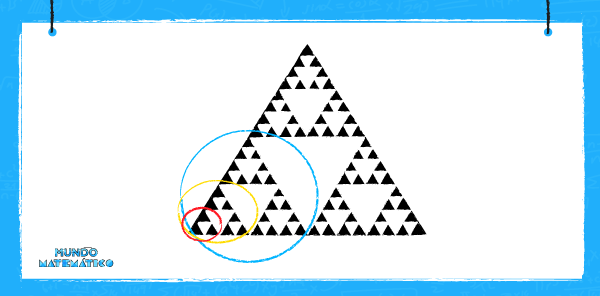
Al observar la imagen notamos un triángulo blanco al centro rodeado de 3 triángulos. Esto se da en cada fragmento y en la figura completa. Para desarrollar el problema comenzaremos marcando los centros de cada triángulo. Al unirlos, obtenemos 4 triángulos iguales. En este caso dejaremos en blanco el triángulo del centro.
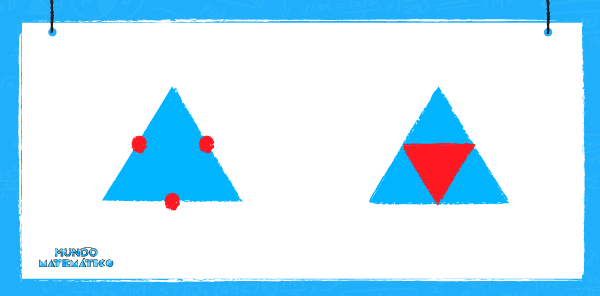
Calculamos el área del total, tomando en cuenta que cada triángulo es un cuarto del área.
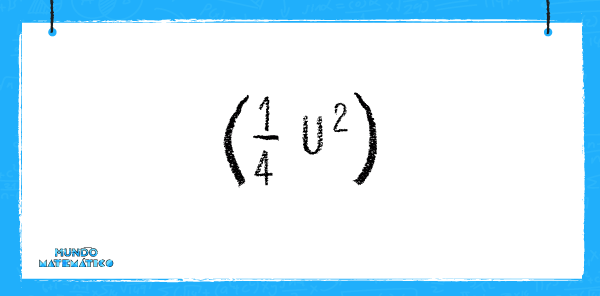
Debido a que son 3 triángulos (no consideramos el blanco del centro), la ecuación sería de la siguiente manera:
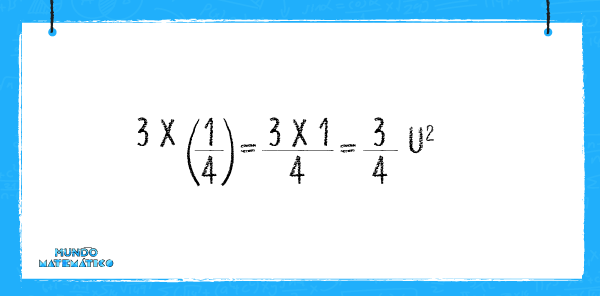
Este proceso se debe aplicar a cada grupo de triángulos:

Tenemos 3 triángulos pintados dentro de 3 triángulos. Esto quiere decir que hay 9 triángulos pintados. Mientras que hay 3 triángulos pintados. Sin embargo en total 16 triángulos lo que quiere decir que cada triángulo equivale a 1/16.

Hallamos el área después de la segunda fragmentación:

Ahora analizamos cómo decrece el área. Después de la primera fragmentación el área es ¾ , mientras que después de la segunda fragmentación obtenemos un área de 9/16 que equivale a (¾)2 .
Esto quiere decir que cada vez que se fragmenta el triángulo, cada uno se multiplica por ¾, es decir 0,75. Si fragmentamos el triángulo por “n” veces, el área sería (¾)n .
Ahora que sabes esto te proponemos crear un juego que tenga nieve. Para ello debes explicar el desarrollo fractal del siguiente copo de nieve:

Para ayudarte a resolver este problema y seguir aprendiendo fractales, no te pierdas este episodio de Mundo Matemático. Puedes disfrutar de cada programa de lunes a viernes a las 8:00 p. m. y los sábados y domingos a las 6:30 p. m. por la señal de Canal IPe.









