Mundo Matemático: La relación entre la velocidad y aceleración

Hay personas que tienen la capacidad de correr a gran velocidad, como los atletas, que en cuestión de segundos pueden recorrer una gran parte de la pista de carreras. Pero hay seres que son más rápidos, como los animales, entre ellos el guepardo, el animal terrestre más rápido que existe. ¿Realmente será tan rápido? ¿Un auto podría ser más rápido que un guepardo? Para resolver estas preguntas Mundo Matemático nos enseñará en qué consiste la velocidad y aceleración. 

Velocidad y Aceleración

La velocidad (v) representa la relación entre la distancia (d) y el tiempo (t) utilizado en el recorrido. Esto se da en el caso del movimiento rectilíneo y se mide en “metros por segundo” (m/s) o en “kilómetros por hora” (km/h).

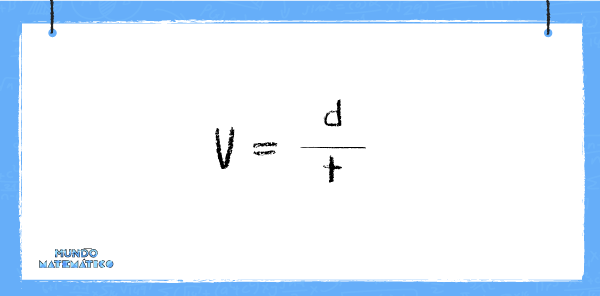
 La velocidad es constante cuando no varía, lo cual se puede evidenciar en tramos cortos. 

La aceleración (v) es el cambio de velocidad (v) en un tiempo determinado. La velocidad inicial (v0) tendrá un valor y la velocidad final (vf) otro, debido a que la velocidad varía.

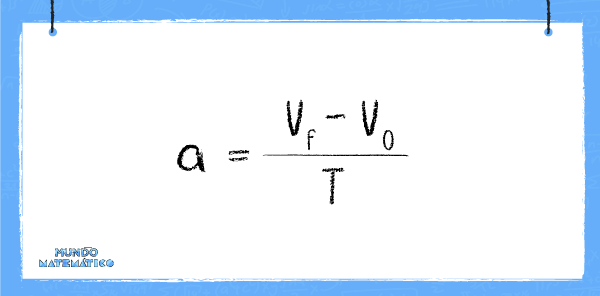
Si el cuerpo está en reposo justo antes de partir, es decir, si el guepardo o un auto parten en reposo, la velocidad inicial es “0”.

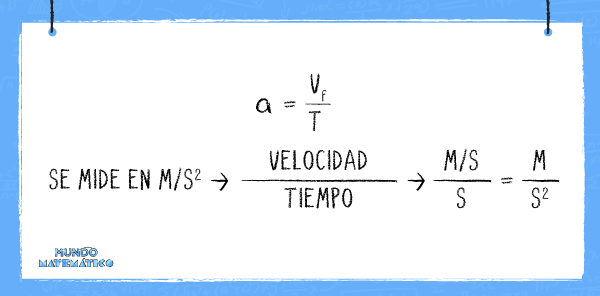
Si la velocidad aumenta en la misma cantidad cada segundo, la aceleración será uniforme. En caso la velocidad disminuya, ocurrirá una desaceleración.

Apliquemos lo aprendido a al siguiente ejemplo:

Imagina que subes a una bicicleta y aceleras de manera uniforme, alcanzando una velocidad de 12 m/s en 3 segundos.  Nuestra aceleración uniforme será:

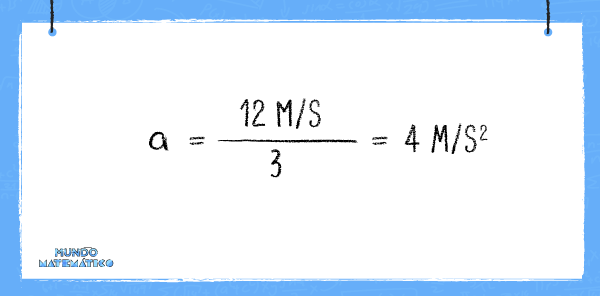
Al relacionar el tiempo con la aceleración, resulta una recta uniforme:

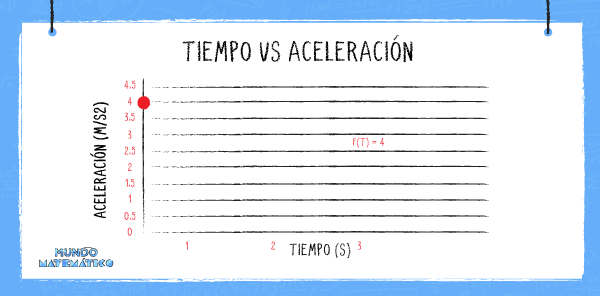
Recordando que “a” es la aceleración y “t” es el tiempo, tenemos que:

a = f(t) = 4

Si se nos dice que la aceleración uniforme es 4 m/s² , significa que por cada segundo que pasa la velocidad va a aumentar en  4 m/s. Así la velocidad inicial será “0”, el primer segundo terminará en 4 m/s, el segundo tendrá al final 8 m/s y el tercer segundo tendrá como velocidad final 12 m/s.

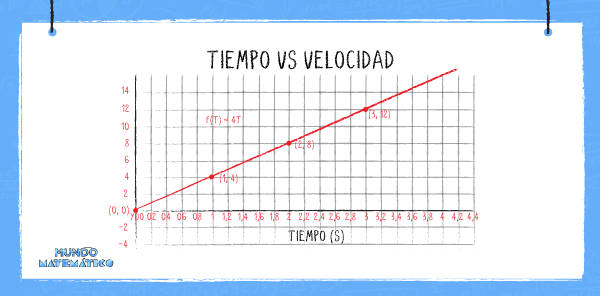
Representamos en un gráfico la velocidad (v), el tiempo y la línea recta que nos muestra la velocidad uniforme:

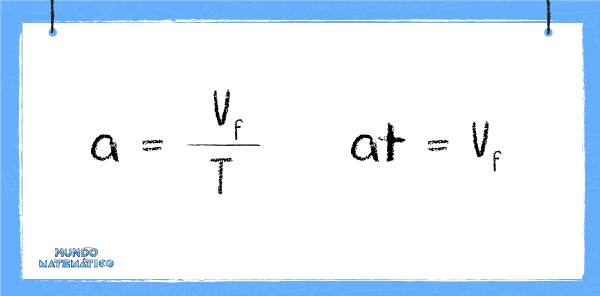
La aceleración (a) se reemplaza por 4 m/s² y la función obtenida es:

v= g (t) = 4t

Distancia

Ahora vamos a calcular la distancia al finalizar el primer segundo, para lo cual promediamos los siguientes valores: 

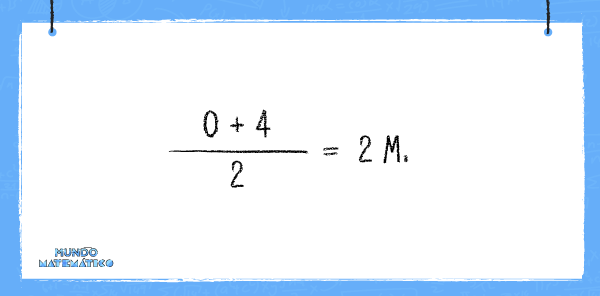
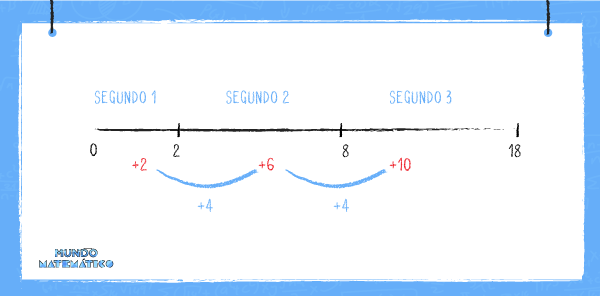
Al finalizar el segundo 2 se habrá recorrido 6 metros. Esta cantidad, sumada a los 2 metros anteriores, dará como resultado 8 metros.

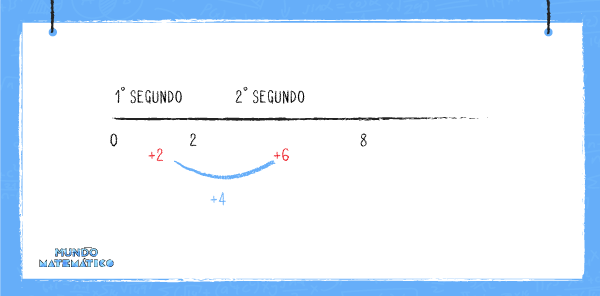
Si continuamos con el tercer segundo, el resultado será el siguiente:

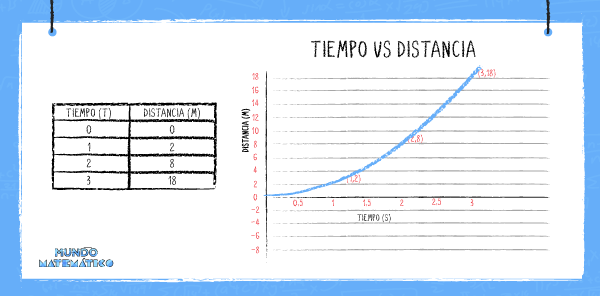
De acuerdo al siguiente gráfico, las distancias recorridas aumentan de forma variada y no lineal. Por esta razón, la línea de crecimiento será una curva:

La relación entre la distancia y el tiempo no es lineal. Aquí aparece una relación cuadrática que se puede desarrollar con la siguiente fórmula:

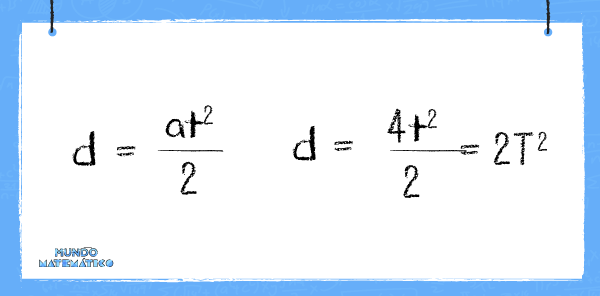
Para resolverlo debemos saber el tiempo y vamos a poder encontrar fácilmente la distancia. 

Si quieres resolver más problemas sobre la velocidad y la aceleración no te pierdas este episodio de Mundo Matemático por la señal de Canal IPe. También puedes verlo en nuestro canal de YouTube. ¡No dejes de verlo!